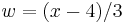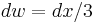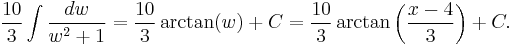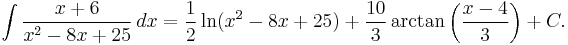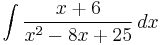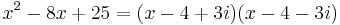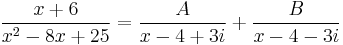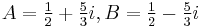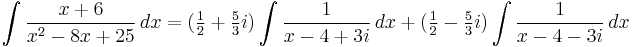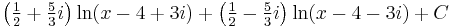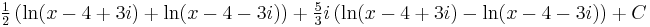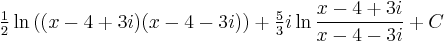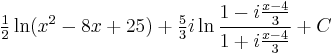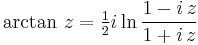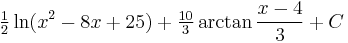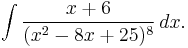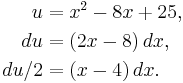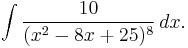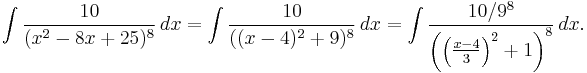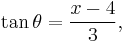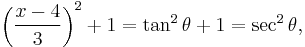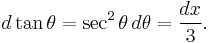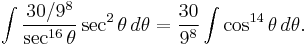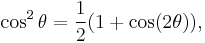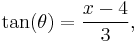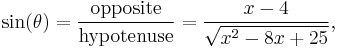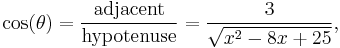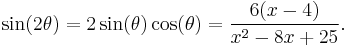Partial fractions in integration
In integral calculus, partial fraction expansions provide an approach to integrating a general rational function. Any rational function of a real variable can be written as the sum of a polynomial function and a finite number of algebraic fractions. Each fraction in the expansion has as its denominator a polynomial function of degree 1 or 2, or some positive integer power of such a polynomial. (In the case of rational function of a complex variable, all denominators will have a polynomial of degree 1, or some positive integer power of such a polynomial.) If the denominator is a 1st-degree polynomial or a power of such a polynomial, then the numerator is a constant. If the denominator is a 2nd-degree polynomial or a power of such a polynomial, then the numerator is a 1st-degree polynomial.
Isaac Barrow's proof of the integral of the secant function was the earliest use of partial fractions in integration.[1] In 1599, Edward Wright gave a solution by numerical methods – what today we would call Riemann sums.
Contents |
A 1st-degree polynomial in the denominator
The substitution u = ax + b, du = a dx reduces the integral
to
A repeated 1st-degree polynomial in the denominator
The same substitution reduces such integrals as
to
An irreducible 2nd-degree polynomial in the denominator
Next we consider such integrals as
The quickest way to see that the denominator x2 − 8x + 25 is irreducible is to observe that its discriminant is negative. Alternatively, we can complete the square:
and observe that this sum of two squares can never be 0 while x is a real number.
In order to make use of the substitution
we would need to find x − 4 in the numerator. So we decompose the numerator x + 6 as (x − 4) + 10, and we write the integral as
The substitution handles the first summand, thus:
Note that the reason we can discard the absolute value sign is that, as we observed earlier, (x − 4)2 + 9 can never be negative.
Next we must treat the integral
First, complete the square, then do a bit more algebra:
Now the substitution
gives us
Putting it all together,
Using complex expanding
In some cases, having certain skill, it's more convenient to use the complex decomposition of the polynomial. So, in the example above:
Expanding the denominator in the two complex multiplier:
Then looking for the expansion of the integrand into two terms
Solving the system of linear equations, we obtain:
After the obvious integration we have:
Grouping the separate real and imaginary terms:
As it's known, the arctangent of a complex variable can be expressed by the logarithm:
This allows us to express the second term in the arctangent:
A repeated irreducible 2nd-degree polynomial in the denominator
Next, consider
Just as above, we can split x + 6 into (x − 4) + 10, and treat the part containing x − 4 via the substitution
This leaves us with
As before, we first complete the square and then do a bit of algebraic massaging, to get
Then we can use a trigonometric substitution:
Then the integral becomes
By repeated applications of the half-angle formula
one can reduce this to an integral involving no higher powers of cos θ higher than the 1st power.
Then one faces the problem of expression sin(θ) and cos(θ) as functions of x. Recall that
and that tangent = opposite/adjacent. If the "opposite" side has length x − 4 and the "adjacent" side has length 3, then the Pythagorean theorem tells us that the hypotenuse has length √((x − 4)2 + 32) = √(x2 −8x + 25).
Therefore we have
and
Notes and references
- ^ V. Frederick Rickey and Philip M. Tuchinsky, "An Application of Geography to Mathematics: History of the Integral of the Secant", Mathematics Magazine, volume 53, number 3, May 1980, pages 162–166
External links
- Partial Fraction Expander
- Mathematical Assistant on Web online calculation of integrals, allows to integrate in small steps (includes partial fractions, powered by Maxima (software))
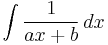
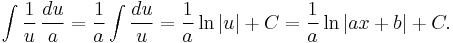
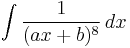
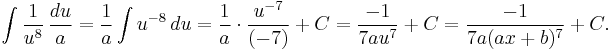
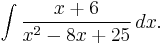
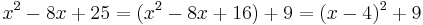
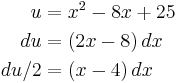
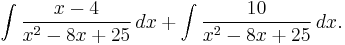
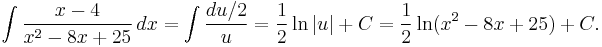
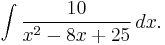
![\begin{align}
& {} \quad \int {10 \over x^2-8x%2B25} \, dx
= \int {10 \over (x-4)^2%2B9} \, dx \\[9pt]
& = \int {10/9 \over \left({x-4 \over 3}\right)^2%2B1}\,dx
= {10 \over 3} \int {1 \over \left({x-4 \over 3}\right)^2%2B1}\, \left({dx \over 3}\right)
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/c7a298021a367541027e9bd0b3b67692.png)